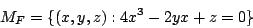
This applet is an interactive rendering of Zeeman's Catastrophe Machine (ZCM), which is a simple mechanical device that represents the cusp catastrophe. The physical setup consists of a wheel, free to rotate about its axis, with two springs connected to a common point on its rim. One of the springs is fastened to a point along the u-axis, while the other is held by hand and freely movable in the uv-plane. The state of the system is the angle θ of the disk relative to the -u-axis when in equilibrium. The system is controlled by the location of the second spring, so the two control parameters are its u and v coordinates. Naturally, the equilibrium angle changes as the control parameters are varied, but what's particularly interesting is that system response is not always smooth: equilibria can vanish, leading to a sudden loss of stability and causing the system to jump to a completely new equilibrium state. This is called a catastrophe. For this system a catastrophe may occur when passing through the star-shaped region in the uv-plane. The system has a single equilibrium outside this region, but three inside (two stable, one unstable).
The potential energy of the system is given by
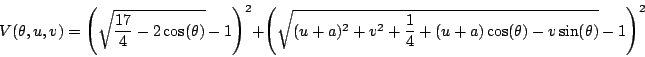
for a wheel diameter of 1, an equilibrium spring lengths of 1, a distance between the end of the top spring and the wheel center of 2, and where a denotes the distance of the wheel center from the origin. One of the cusps occur at the origin. In a neighborhood of that point there exists diffeomorphisms x,y, and z and a smooth function w,such that, in that neighborhood, the potential has the functional form
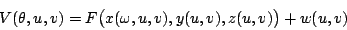
where the function F is given by
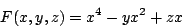
which is called the cusp and is one of Thom's seven elementary catastrophes. Here, x is the state variable, while y and z are the control parameters.
The catastrophe surface of the cusp is given by the set of points (x,y,z) that are critical points of F for constant control parameters (that is, the extrema of the potential function) and is given by
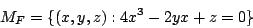
which is the following surface in 3-space:
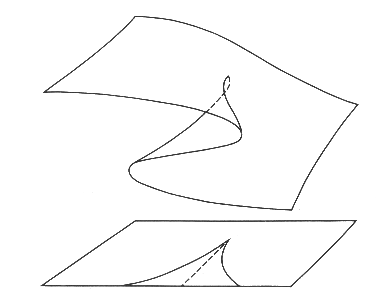
The castrophe set is the subset of the above surface which consists of those critical points that are degenerate, that is, where the second derivative also vanishes. These points define where local minima are created and destroyed and thus dictate the "interesting" behavior of the potential as control parameters vary. This set is given by
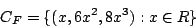
Finally, there is the bifuraction set, which is the projection of the catastrophe set onto the control parameters. It is given simply by
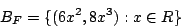
and its shape is the reason for calling this catastrophe the cusp.
The cusp is such an interesting catastrophe because it possesses the features of bimodality and hysteresis, that is, there are two equilibrium positions, but which state the system ends up in depends on the path taken through parameter space. What is also interesting to note is that the system is all the time governed by a smooth potential function. The catastrophe surface and set are also smooth. However, the projection of a smooth object down onto the plane (the bifurcation set) develops singularities which drive the interesting behavior of the system. This is a common theme throughout nonlinear dynamics.
Finally, the ZCM also gives rise to interesting dynamical behavior when periodically driven, rather than moved quasistatically. In fact, the driven ZCM displays a period doubling route to chaos and a chaotic attractor based on the parameters of the driving term. A good discussion of this chaotic dynamical behavior can be found in the article T. J. Litherland, and A. Siahmakoun, Chaotic Behavior of the Zeeman Catastrophe Macine, Am. J. Phys. 63, 426 (1995).